Reaktionsfunktionen und Isoprofitkurven

(Link von der Seite Marktgleichgewicht: Warum Lösungen "off the curve" zustandekommen können; Erklärung von "Isoprofikurven".)

(Link von der Seite Modell von Cournot: Warum sich ein Kartell für die Dupolisten rechnet.)

Dass sie sich verbessern können, lässt sich grafisch recht anschaulich mithilfe von Reaktionsfunktionen darstellen, die aus Isoprofitkurven gewonnen werden.

Preisabsatzfunktion der beiden Duopolisten (ohne Kosten):

$$ p = a -b(x_1 + x_2) \tag{1} $$

Umsatz- bzw. Gewinnfunktion für Unternehmer 1:

$$ U_1 = G_1 = ax_1 - b{x_1}^2 - bx_1x_2 \tag{2} $$

Um Isogewinnkurven konstruieren zu können, wird der Gewinn auf einen konstanten Wert $g$ gesetzt und (2) nach $x_2$ aufgelöst:

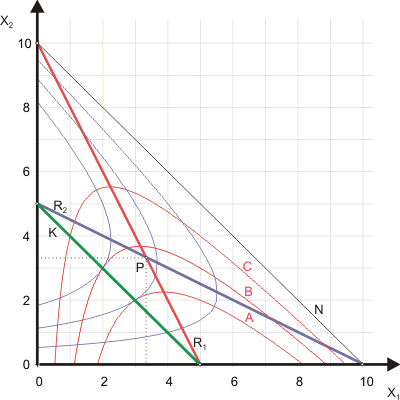
$$ x_2 = \cfrac{a}{b} - x_1 - \cfrac{g}{bx_1} \tag{3} $$

Wie Abbildung 3 zeigt, interessiert Anbieter 1 für ein gegebenes Angebot von Anbieter 2 das Maximum einer Isogewinnkurve, da durch das Maximum die den höchsten erreichbaren Gewinn anzeigende Isoprofitkurve determiniert wird. Also wird die notwendige Bedingung für ein Maximum gesucht:

$$ \cfrac{\text{d}x_2}{\text{d}x_1} = -1 + \cfrac{bg}{(bx_1)^2} \overset{!}{=} 0 \tag{4} $$

Aufgelöst nach $g$ findet man unter Verwendung von (3) die Reaktionsfunktion R₁*

$$ x_2 = \cfrac{a}{b} - 2x_1 \tag{5} $$

Sie verbindet die Maxima der Isogewinnkurven von Anbieter 1 (vgl. Abbildung 3).

Um die Iso-Null-Gewinn-Kurve zu bestimmen, wird in (3) $g = 0$ gesetzt:

$$ x_2 = \cfrac{a}{b} - x_1 \tag{6} $$

Auf ihr wird die Sättigungsmenge angeboten (Gerade N in Abbildung 3).

Maßstabsgetreue Darstellung:

Die nachstehenden Abbildungen zeigen das Cournotsche Mineralwasserduopol, wenn in der Preis-Absatz-Funktion (1) $a = 10$ und $b = 1$ gesetzt werden. In den Abbildungen sind negative Gewinnsituationen, die theoretisch entstehen, wenn das Angebot die Sättigungsmenge übersteigt, nicht dargestellt (weil ein negativer Preis hier auch wenig Sinn macht).

Abbildung 1

Gewinngebirge des Anbieters 1. In der Ebene sind ausgewählte Isoprofitkurven zu erkennen. "Tiefere" Isoprofitkurven zeigen einen höheren Gewinn. Die blaue Linie zeigt die Reaktionsfunktion. Rot erkennt man die Umsatzparabel als Schnitt durch das Gebirge, wenn Duopolist 2 nichts anbietet und Duopolist 1 wie ein Monopolist handeln kann.

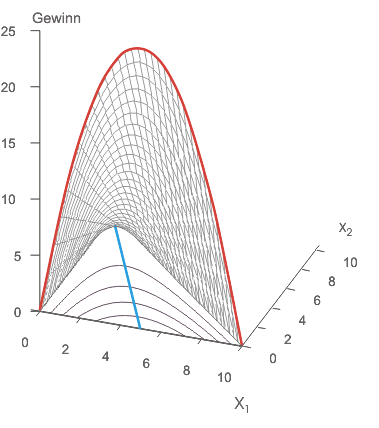
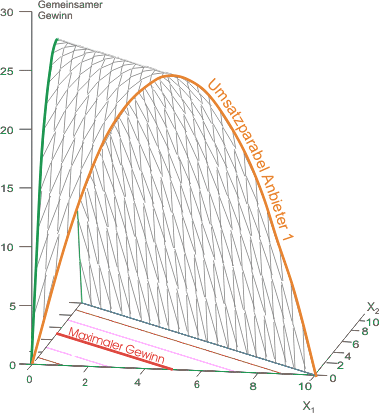
Dargestellt wird der Gewinn des Anbieters 1 in Abhängigkeit von den Angebotsmengen beider Anbieter. Bietet Anbieter 2 nichts an ($x_2=0$), dann erkennt man über der $x_1$-Achse die gewöhnliche Umsatzparabel (des Monopolisten, rot hervorgehoben). Für steigende Angebotsmengen "schrumpfen die Umsatzparabeln zusammen". Man blickt quasi in einen Tunnel, der - durch nacheinander aufgestellte Parabeln gebildet - immer enger wird und schließlich im Punkt ($x_1 = 0$, $x_2 = 10$) als Sackgasse endet, da hier Anbieter 2 die Sättigungsmenge anbietet.

Die eingezeichnete Reaktionsfunktion zeigt den auf die Mengenebene projizierten "Kamm des Gewinngebirges". Die Isogewinnlinien sind die Höhenlinien des "Gebirges".

Abbildung 2

Hier wird der Gesamtgewinn ($G_1 +G_2$) dargestellt, also die Summe des Gebirges aus Abbildung 1 und des entsprechenden Gebirges des Anbieters 2, das dem des Anbieters 1 gleicht. Der maximale Kartellgewinn in Höhe von 25 wird erreicht, wenn beide Anbieter zusammen die Menge 5 anbieten. Die Isogewinnlinien für das Kartell sind Geraden, die parallel zur rot eingezeichneten Isogewinnlinie für den Monopolgewinn verlaufen.

Abbildung 3

Für beide Anbieter sind die Isogewinnkurven für Gewinne in Höhe von 5, 10 und 15 eingezeichnet. Da sich die Gewinne auf 25 (=Monopolgewinn) addieren lassen, tangieren sich die entsprechenden Isogewinnkurven auf der Kartelllinie (grün). Keiner der beiden Anbieter kann hier eine höhere Isogewinnkurve erreichen, ohne dass nicht der andere Gewinneinbußen hinzunehmen hätte (Pareto-Kriterium erfüllt). Der Schnittpunkt der Reaktionskurven $R_1$ und $R_2$ liegt bei ($x_1 = x_2 = 3,33$). Da sich die Isogewinnlinien der Anbieter in diesem Punkt schneiden (nicht eingezeichnet), könnte ein Anbieter mehr Gewinn machen, ohne dass der andere Gewinn einbüßen müsste, wenn sie sich in Richtung Kartelllinie bewegen würden. N zeigt die Nullgewinnsituation, wenn beide Anbieter zusammen die Sättigungsmenge auf den Markt bringen.